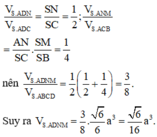Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AM\) (1)
Tam giác SAB vuông cân tại A (do SA=SB=a)
\(\Rightarrow AM\perp SB\) (trung tuyến đồng thời là đường cao) (2)
(1);(2)\(\Rightarrow AM\perp\left(SBC\right)\Rightarrow AM\perp SC\)
Hoàn toàn tương tự ta có \(AN\perp SC\)
\(\Rightarrow SC\perp\left(AMN\right)\Rightarrow\left(SAC\right)\perp\left(AMN\right)\)
Từ A kẻ \(AH\perp SC\Rightarrow H\in\left(AMN\right)\)
Lại có \(SA\perp\left(ABCD\right)\Rightarrow\left(SAC\right)\perp\left(ABCD\right)\)
\(\Rightarrow\widehat{HAC}\) là góc giữa (AMN) và (ABCD)
\(AC=a\sqrt{2}\) ; \(SC=a\sqrt{3}\)
\(sin\widehat{HAC}=cos\widehat{SCA}=\dfrac{AC}{SC}=\sqrt{\dfrac{2}{3}}\Rightarrow\widehat{HAC}\approx54^044'\)
Đáp án C.
Hướng dẫn giải:
Ta có
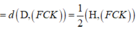
Kẻ H I ⊥ C K , H J ⊥ F I
Ta có H I = 2 a 5 5
⇒ S B = a 3
⇒ H F = a 2 2
Ta có 1 H J 2 = 1 H I 2 + 1 H F 2 = 13 4 a 2
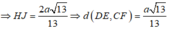
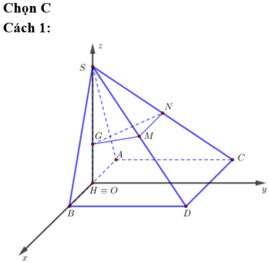
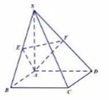
Chọn hệ trục tọa độ Oxyz như hình vẽ. Khi đó
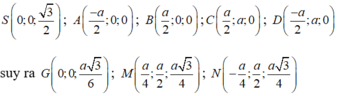
Ta có mặt phẳng (ABCD) có vectơ pháp tuyến là 
, mặt phẳng (GMN) có vectơ pháp tuyến là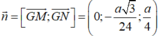 
Gọi (α) là góc giữa hai mặt phẳng (GMN) và (ABCD), ta có
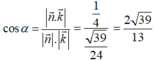
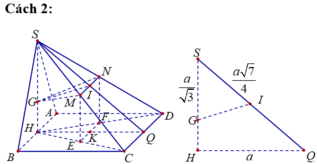
Gọi E, F lần lượt là hình chiếu của M và N lên (ABCD). Suy ra E, F lần lượt là trung điểm của HC, HD.
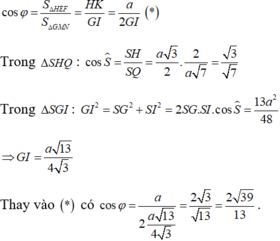
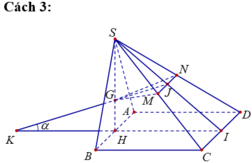
Gọi H, I lần lượt là trung điểm của AB, CD.
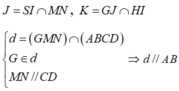
Mà d ⊥ (SIH) nên góc giữa góc giữa hai mặt phẳng (GMN) và (ABCD) là 
Đáp án B
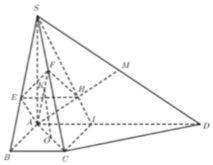
Ta có: B C ⊥ A B B C ⊥ S A ⇒ B C ⊥ M A
Mặt khác A M ⊥ S B ⇒ A M ⊥ S B C ⇒ A N ⊥ S C , tương tự A N ⊥ S C
Do đó S C ⊥ A M N , mặt khác ∆ S B C vuông tại B suy ra tan B S C ^ = B C S B = a S A 2 + A B 2 = 1 3
⇒ S B ; S C ^ = B S C ^ = 30 ° ⇒ S B ; A M N ^ = 60 ° .
Chọn C.
Phương pháp:
- Chứng minh tứ giác AEFH nội tiếp, từ đó tìm tâm đường tròn ngoại tiếp tam giác EHF .
- Tìm đỉnh hình nón và tính chiều cao, bán kính đáy rồi suy ra thể tích.
Cách giải:
Chọn đáp án C.
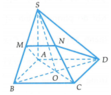
Gọi O là tâm của hình vuông ABCD thì B D ⊥ S A O
