Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi O là giao điểm của AC và BD
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔABD có
AO,DM là các đường trung tuyến
AO cắt DM tại G
Do đó: G là trọng tâm của ΔABD
b: Xét ΔABD có
AO là đường trung tuyến
G là trọng tâm
Do đó: \(AG=\dfrac{2}{3}\cdot AO=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AC=\dfrac{1}{3}AC\)
Ta có: CG+GA=CA
=>\(GA+\dfrac{1}{3}AC=AC\)
=>\(GA=\dfrac{2}{3}AC\)
\(\dfrac{AG}{GA}=\dfrac{\dfrac{1}{3}AC}{\dfrac{2}{3}AC}=\dfrac{1}{3}:\dfrac{2}{3}=\dfrac{1}{2}\)
=>GA=2AG

( Bạn tự vẽ hình nha )
a) Xét tứ giác AEDF có :
DE // AB
DF // AC
=> AEDF là hình bình hành ( dấu hiệu nhận biết )
Xét hình bình hành AEDF có :
AD là phân giác của góc BAC
=> EFGD là hình thoi ( dấu hiệu nhận biết )
b) XÉt tứ giác EFGD có :
FG // ED ( AF //ED )
FG = ED ( AF = ED )
=> EFGD là hình bình hành ( dấu hiệu nhận biết )
c) Nối G với I
+) XÉt tứ giác AIGD có :
F là trung điểm của AG
F là trung điểm của ID
=> AIGD là hình bình hành ( dấu hiệu nhận biết )
=> GD // IA hay GD // AK ( tính chất )
+) Xét tứ giác AKDG có :
GD // AK
AG // Dk ( AF // ED )
=> AKDG là hình bình hành ( dấu hiệu )
+) xtes hinhnf bình hành AKDG có :
AD và GK là 2 đường chéo
=> AD và GK cắt nhau tại trung điểm mỗi đường
Mà O là trung điểm của AD ( vì AFDE là hình thoi )
=> O là trung điểm của GK
=> ĐPCM

a: Xét tứ giác AMCn có
AM//Cn
AM=CN
=>AMCN là hình bình hành
b; Xét ΔBAE có
M là trung điểm của BA
MF//AE
=>F là trung điểm của BE
=>BF=FE
Xét ΔDFC có
N là trung điểm của DC
NE//FC
=>E là trung điểm của DF
=>DE=EF=FB

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

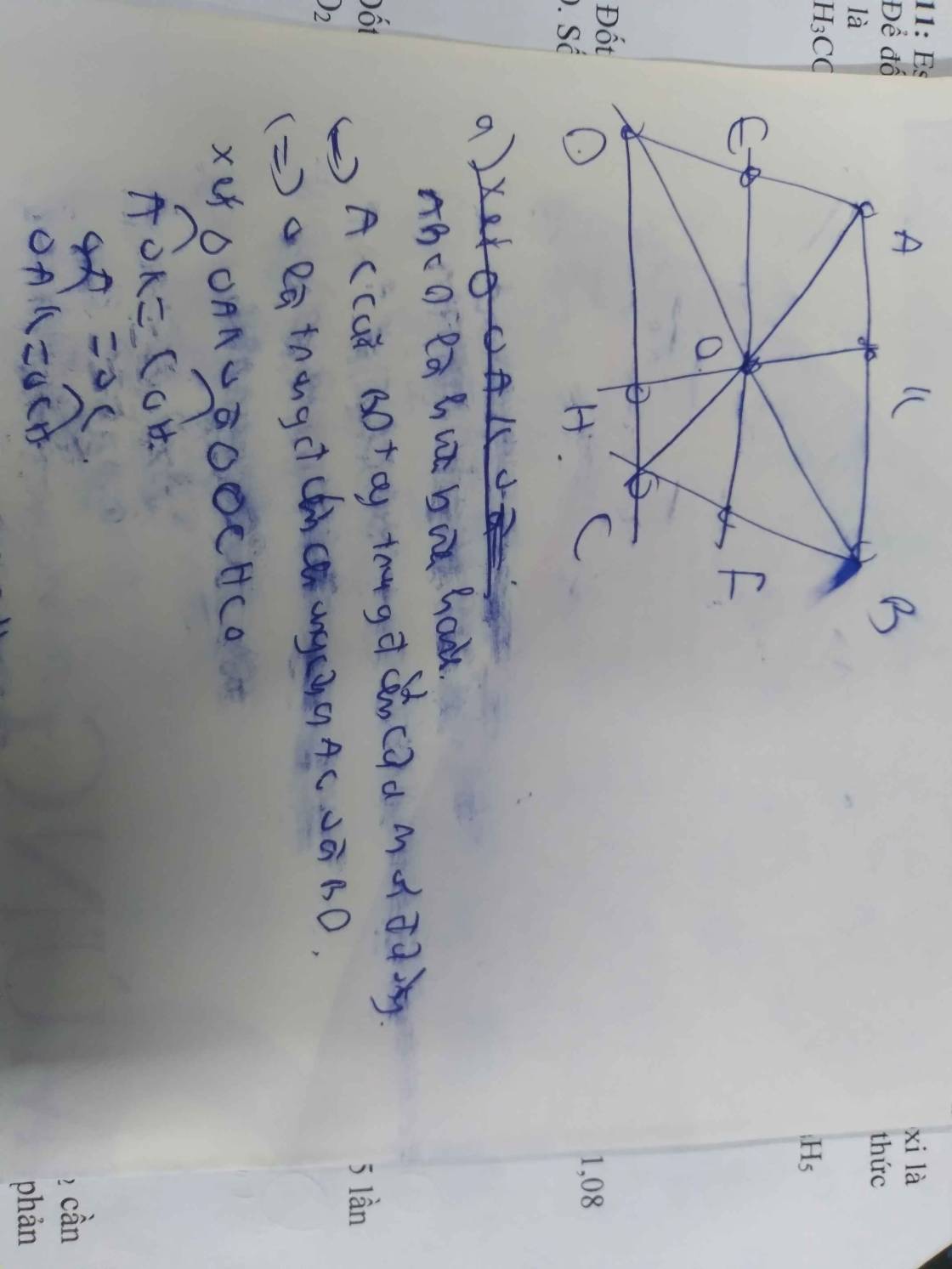



a: Gọi O là giao điểm của AC và BD
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
XétΔABD có
DM,AO là các đường trung tuyến
DM cắt AO tại G
Do đó: G là trọng tâm của ΔABD
b: XétΔABD có
G là trọng tâm
AO là đường trung tuyến
Do đó: \(GA=\dfrac{2}{3}AO=\dfrac{2}{3}\cdot\dfrac{1}{2}\cdot AC=\dfrac{1}{3}AC\)
GA+GC=AC
=>\(GC+\dfrac{1}{3}AC=AC\)
=>\(GC=\dfrac{2}{3}AC\)
\(\dfrac{GC}{GA}=\dfrac{\dfrac{2}{3}AC}{\dfrac{1}{3}AC}=\dfrac{2}{3}:\dfrac{1}{3}=2\)
=>GC=2GA
c: Xét ΔGAI và ΔGCK có
\(\widehat{GAI}=\widehat{GCK}\)(hai góc so le trong, AI//CK)
\(\widehat{AGI}=\widehat{CGK}\)
Do đó: ΔGAI đồng dạng với ΔGCK
=>\(\dfrac{GA}{GC}=\dfrac{GI}{GK}\)
=>\(\dfrac{GI}{GK}=\dfrac{1}{2}\)(1)
Xét ΔAEG và ΔCFG có
\(\widehat{AEG}=\widehat{CFG}\)
\(\widehat{AGE}=\widehat{CGF}\)
Do đó: ΔAEG đồng dạng với ΔCFG
=>\(\dfrac{GA}{GC}=\dfrac{GE}{GF}=\dfrac{1}{2}\left(2\right)\)
Từ (1) và (2) suy ra \(\dfrac{GI}{GK}=\dfrac{GE}{GF}\)
Xét ΔGIE và ΔGKF có
\(\dfrac{GI}{GK}=\dfrac{GE}{GF}\)
\(\widehat{IGE}=\widehat{KGF}\)
Do đó: ΔGIE đồng dạng với ΔGKF
=>\(\widehat{GIE}=\widehat{GKF}\)
mà hai góc này là hai góc ở vị trí so le trong
nên EI//FK