Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước 1: Vẽ đường thẳng \(d_1: y-2x=2\) đi qua (0;2) và (-1;0).
Lấy điểm O(0;0) không thuộc \(d_1\). Vì 0-2.0=0<2 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(y - 2x \le 2\) là nửa mp bờ \(d_1\), chứa điểm O.
Bước 2: Vẽ đường thẳng \(d_2: y=4\) đi qua (0;4) và (1;4).
Lấy điểm O(0;0) không thuộc \(d_2\). Vì 0<4 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(y \le 4\) là nửa mp bờ \(d_2\), chứa điểm O.
Bước 3: Vẽ đường thẳng \(d_3: x=5\) đi qua (5;0) và (5;1).
Lấy điểm O(0;0) không thuộc \(d_3\). Vì 0<5 nên O thuộc miền nghiệm
Miền nghiệm của BPT \(x \le 5\) là nửa mp bờ \(d_3\), chứa điểm O.
Bước 4: Vẽ đường thẳng \(d_4: x + y = - 1\) đi qua (-1;0) và (0;-1).
Lấy điểm O(0;0) không thuộc \(d_4\). Vì 0+0=0>-1 nên O thuộc miền nghiệm.
Miền nghiệm của BPT \(x + y \ge - 1\) là nửa mp bờ \(d_4\), chứa điểm O.
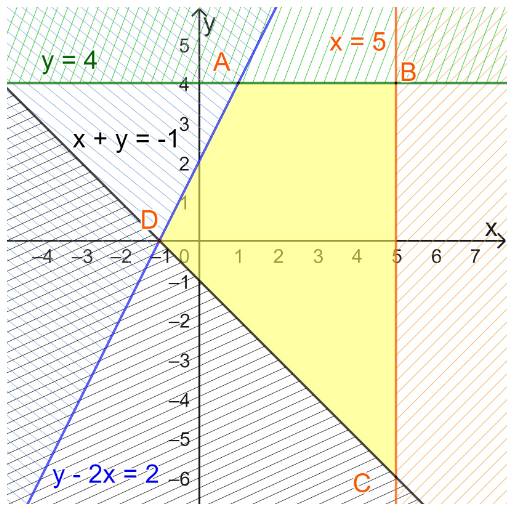
Miền biểu diễn nghiệm của hệ bất phương trình là miền tứ giác ABCD với
A(1;4); B(5;4), C(5;-6); D(-1;0).
Giá trị F tại các điểm A, B, C, D lần lượt là:
\(F\left( {1;4} \right) = - 1 - 4 = - 5\)
\(F\left( {5;4} \right) = - 5 - 4 = - 9\)
\(F\left( {5;-6} \right) = - 5 - (-6) = 1\)
\(F\left( { - 1;0} \right) = - \left( { - 1} \right) - 0 = 1\)
Vậy giá trị lớn nhất của biểu thức F(x;y) là 1 và giá trị nhỏ nhất của biểu thức F(x;y) là -9.

gọi T là tập hợp giá trị của F
\(\begin{cases}\sqrt[3]{x}\left(\sqrt[3]{x}-1\right)+\sqrt[3]{y}\left(\sqrt[3]{y}-1\right)=\sqrt[3]{xy}\\\sqrt[3]{x}+\sqrt[3]{y}+\sqrt[3]{xy}=m\end{cases}\)
Đặt S = \(\sqrt[3]{x}+\sqrt[3]{y},P=\sqrt[3]{xy}\) điều kiện \(S^2\ge4P\)hệ 1 trở thành
\(\begin{cases}S^2-S-3P=0\\S+P=m\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}S^2+2S-3m=0\\P=m-s\end{cases}\)\(\Leftrightarrow\)\(\begin{cases}m=\frac{S^2+2S}{3}\\P=\frac{S^2-S}{3}\end{cases}\)
Ta có \(S^2\ge4P\Leftrightarrow S^2\ge\frac{4S^2-4S}{3}\Leftrightarrow s^2-4S\le0\Leftrightarrow0\le S\le4\)
từ đó , hệ 1 có nghiệm \(\Leftrightarrow\)hệ 2 có nghiệm (S;P) thỏa mãn \(S^2\ge4P\Leftrightarrow\)phương trình \(S^2+2S-3m=0\)có nghiệm S thỏa mãn điều kiện 0\(0\le S\le4\)tức là
\(\Delta'=1+3m\ge0\)và \(\left[\begin{array}{nghiempt}0\le-1-\sqrt{1+3m}\le4\\0\le-1+\sqrt{1+3m}\le4\end{array}\right.\)\(\Leftrightarrow\)\(\begin{cases}m\ge-\frac{1}{3}\\1\le\sqrt{1+3m}\le5\end{cases}\)\(\Leftrightarrow\)\(0\le m\le8\)
vậy max F=8, min=0

\(\left(x^3+y^3\right)\left(x+y\right)=xy\left(1-x\right)\left(1-y\right)\Leftrightarrow\left(\frac{x^2}{y}+\frac{y^2}{x}\right)\left(x+y\right)=\left(1-x\right)\left(1-y\right)\left(1\right)\)
Ta có : \(\left(\frac{x^2}{y}+\frac{y^2}{x}\right)\left(x+y\right)\ge4xy\)
và \(\left(1-x\right)\left(1-y\right)=1-\left(x+y\right)+xy\le1-2\sqrt{xy}+xy\)
\(\Rightarrow1-2\sqrt{xy}+xy\ge4xy\Leftrightarrow0\) <\(xy\le\frac{1}{9}\)
Dễ chứng minh : \(\frac{1}{1+x^2}+\frac{1}{1+y^2}\le\frac{1}{1+xy};\left(x,y\in\left(0;1\right)\right)\)
\(\frac{1}{\sqrt{1+x^2}}+\frac{1}{\sqrt{1+y^2}}\le\sqrt{2\left(\frac{1}{1+x^2}+\frac{1}{1+y^2}\right)}\le\sqrt{2\left(\frac{2}{1+xy}\right)}=\frac{2}{\sqrt{1+xy}}\)
\(3xy-\left(x^2+y^2\right)=xy-\left(x-y\right)^2\le xy\)
\(\Rightarrow P\le\frac{2}{\sqrt{1+xy}}+xy=\frac{2}{\sqrt{1+t}}+t\), \(\left(t=xy\right)\), (0<\(t\le\frac{1}{9}\)
Xét hàm số :
\(f\left(t\right)=\frac{2}{\sqrt{t+1}}+t\) , (0<\(t\le\frac{1}{9}\)
Ta có Max \(f\left(t\right)=f\left(\frac{1}{9}\right)=\frac{6\sqrt{10}}{10}+\frac{1}{9}\), \(t\in\left(0;\frac{1}{9}\right)\)

Đặt \(A\left(3,4\right),B\left(x,y\right),N\left(0,y\right),M\left(x,0\right)\).
Khi đó \(f\left(x,y\right)=\sqrt{\left(x-3\right)^2+\left(y-4\right)^2}+\left|x\right|+\left|y\right|\)
\(=BA+BM+BN\)
\(\ge BA+BO\)
\(\ge AO\)(theo bđt tam giác)
Dấu \(=\)khi \(B\equiv O\)suy ra \(x=y=0\).
Vậy \(minf\left(x,y\right)=f\left(0,0\right)=5\).